Beaucoup d’étudiants ont du mal a déterminer ou justifier de la taille d’un échantillon dans une enquête par sondage. En théorie, plus la taille de l’échantillon est importante, plus la marge d’erreur est réduite et donc plus les résultats sont précis. Vous pouvez facilement visualiser cela grace à un petit applicatif fourni par Sphinx sur son site.
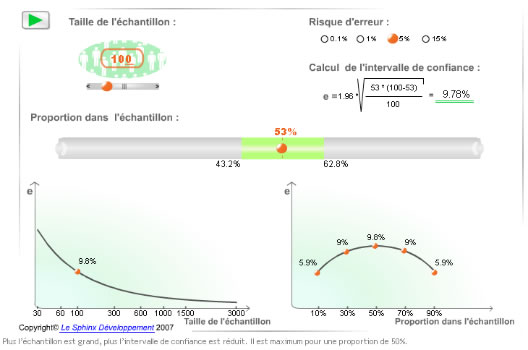
Dans cet exemple, avec un échantillon fixé à 100 personnes, si par exemple 53% déclarent être parties lors des dernières vacances, la marge d’erreur sera de + ou – 9,78%, ce qui signifie en fait qu’il y a entre 43,2% (53% – 9,78%) et 68,8% (53% + 9,78%) des personnes qui sont parties en vacances.
Si maintenant je double la taille de mon échantillon en interrogeant 200 personnes (déplacer le curseur en haut à gauche à 200 ou taper 200) on constate que l’erreur d’échantillonnage passe de 9,78% à 6,92%.
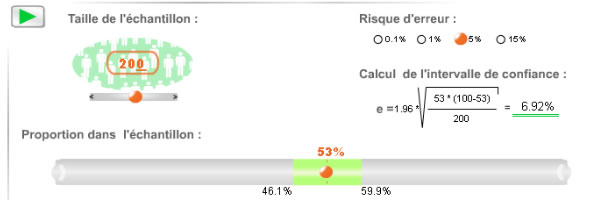
On a donc bien vérifié que plus la taille de l’échantillon augmente, plus l’erreur d’échantillonnage diminue et donc plus les résultats sont précis. Cependant, pour diviser par deux l’erreur d’échantillonnage, et donc passer de 9,78% à 4,89%, il faudra interroger 4 fois plus de personnes, donc 4 x 100 = 400.
Le risque d’erreur ou interval de confiance.
 En haut à droite du simulateur Sphinx vous voyez mentionné le risque d’erreur qu’on appelle aussi interval de confiance. Dans les sondages d’opinion, on travaille avec un interval de 5%. Pour simplifier, cela signifie que si vous faites 100 sondages dans des conditions similaires, dans 95% des cas vous aurez la même fourchette de résultats (% de départ en vacances + – marge d’erreur), et dans 5% des cas, le sondage vous trompera en indiquant un autre résultat. C’est une sorte de phénomène aléatoir qui peut arriver un jour à tous les sondeurs.
En haut à droite du simulateur Sphinx vous voyez mentionné le risque d’erreur qu’on appelle aussi interval de confiance. Dans les sondages d’opinion, on travaille avec un interval de 5%. Pour simplifier, cela signifie que si vous faites 100 sondages dans des conditions similaires, dans 95% des cas vous aurez la même fourchette de résultats (% de départ en vacances + – marge d’erreur), et dans 5% des cas, le sondage vous trompera en indiquant un autre résultat. C’est une sorte de phénomène aléatoir qui peut arriver un jour à tous les sondeurs.
Cet interval de confiance détermine la formule qui en l’occurrence sera :
n = taille de l’échantillon
p = probabilité de réponse positive
q = = 1-p
E = erreur acceptée
Erreur d’échantillonnage (E) = +/- 1.96 x racine (pq)/ n
Avec ici p = 0.53
Q = 1 – 0.53 = 0.47
Dans les fait on arrondit souvent 1.96 à 2, ce qui permet en travaillant la formule de calculer une taille d’échantillon de la manière suivante.
4 pq
n > ——
(E)2
Si p est connu : si p inconnu : on pose p = 0,5
Dans les faits, les sondeurs ne calculent pas la marge d’erreur. Il s’appuie sur des pratiques de la preofession et interviewent le plus souvent entre 400 à 600 personnes pour les sondages locaux, et de 800 à 1000 pour les sondages nationaux.
Dans la cadre de vos travaux d’étudiants
Un étudiant, dans le cadre de son PDUC, n’a pas les moyens ou le temps d’interroger un grand nombre de personnes et le plus souvent il devra se contenter d’un petit échantillonnage de 100 personnes. Sachez que cela ne discrédite en rien la qualité de votre travail. Les indications que vous observerez sur le marché ou votre clientèle restent tout aussi probants. Simplement, ils ne constituent que des indicateurs qui faute d’une plus grande précision, doivent être appuyés par d’autres éléments d’investigation.
Enfin, le plus important n’est pas la taille de l’échantillon mais la qualité de votre questionnaire. Si vos questions sont pertinentes, si elle intéressent votre interlocuteur alors les réponses apportées seront pertinentes.
Vous avez des question ? Rendez vous dans le forum du BTS MUC
salut je m’appelle gagnesiry je suis étudiante sénégalaise je fais comme filiére marketing . en faite je voulais faire un commentaire mais est ce qu’ il ne serait pas mieux de nous donner plus de détail pour accéder au forum des étudiants en BTS
Je ne savais que la détermination de la taille d’un échantillon était aussi scientifique !
je suis un etudiant ivoirien admissible au BTS option Gestion Commerciale, je voudrais vous remercier pour ces informations mais cela nous sera encore plus utile si vous publiez toutes les corrections de vos examens comme celui du BTS MUC dossier ACRC en cours apres evidemment la composition. merci.
d’où est tirer cette formule
je dois soutenir une these en pharmacie et j’ai utiliser cette formule incluant le risque d’erreur, l’intervazl de confiance , le p et le q mais je veux connaitre la source de cette formule. d’ou est elle tirer?
je ne comprend pas comment on calcule la taille de l’échantillon, il n’y a pas de formule?
Je suis Luvalya Venant, etudiant, Congolais (DRC) a l Universite Officielle de Ruwenzori en ville de Butembo. Je fais la Faculte des Sciences Economiques et de Gestion, 3e Graduat.
Merci pour nous avoir disponibiliser la formule; cependant ma preocupation reste la suivante: Mon constat c est que cette formule reste peut etre d usage en cas ou l on veut faire l enquete au sein d une grande population.
Mais alors, qu en est il si son enquete concerne par exemple certaines institutions au sein d une seule ville; Les quells pour y acceder a des donnees, il faut beucoup des gymnastiques?
Merci d avance pour la suite favorable que vous me reservez